Appinio Research · 06.03.2023 · 18min Tiempo de lectura
Ya sea que se traten sobre perspectivas políticas, la satisfacción del cliente, insights de Appinio o de una investigación sobre los empleados de una empresa: a través de los estudios es posible conocer el sentimiento, las opiniones, las creencias y las tendencias del público. Y, por supuesto, a cuanta más personas entrevistes, más cerca estarás de obtener un resultado representativo. Pero, imagina consultar a todas las personas de España para saber a quién votarían en las próximas elecciones... ¡imposible!
Aquí es donde surge la necesidad de una muestra representativa.
Una muestra representativa se centra en una parte de la población y pretende reflejar las opiniones del público en general. Pero, particularmente en la investigación mediante estudios, ¿qué variables debes tener en cuenta? ¿Cómo sabes cuántos participantes necesitas para asegurarte de consultar a una muestra representativa de la población? En este artículo, te mostraremos qué valores clave necesitas para calcular la muestra perfecta para tu estudio y que tus resultados representen fielmente a la población.
¿Quieres calcular rápidamente el tamaño de la muestra para tu estudio teniendo ya todos los valores clave? Utiliza nuestra calculadora online para determinar la muestra que necesitas.
Calculadora de tamaño de muestra
Utiliza nuestra calculadora para comprobar rápidamente el tamaño de la muestra de tu estudio. Sólo tienes que introducir tus valores y verificar el resultado. Todas las métricas utilizadas en la calculadora se explican en detalle más adelante en el artículo. Si tienes más preguntas, no dudes en ponerte en contacto con nuestros expertos a través del chat.
Definición: ¿Qué es una muestra?
Una muestra es una pequeña porción o cantidad que pretende demostrar cómo es el todo.
Hay varios métodos diferentes de muestreo que se pueden utilizar, por ejemplo, podrías optar por utilizar una "muestra aleatoria", en la que los participantes son elegidos totalmente al azar entre la población en general, por lo que todos los miembros de la población tienen las mismas posibilidades de ser seleccionados para tu estudio.
Una muestra aleatoria es útil cuando se realiza una investigación de mercados exploratoria o se recopilan nuevas ideas, pero no sería útil si quisieras saber cuántos españoles son veganos, ya que tu muestra aleatoria podría excluir a algunos participantes (p. ej. no hay suficientes mujeres) o incluir a demasiadas personas del mismo grupo (p. ej. demasiados Millennials), ocasionando que no puedas extraer ideas aplicables a tu público objetivo deseado o a la población general.
Por qué es importante el tamaño de la muestra
Especialmente en la investigación a través de estudios, una muestra debe cumplir una serie de criterios específicos e incluir a todos los distintos grupos -como mujeres, hombres o diversos grupos de edad- en la misma proporción que la población a la que se quiere representar. Además, la muestra debe ser lo suficientemente grande no sólo para ser representativa, sino también para hacer afirmaciones fiables. Al elegir una muestra es importante comprobar su fiabilidad; si la muestra es demasiado pequeña, la información recogida puede ser parcial; por otra parte, si la muestra es demasiado grande, sería un despilfarro de recursos. Cuanto mayor sea el grupo, más se acercarán los resultados al mercado objetivo, y menos factores de azar, errores y declaraciones falsas podrán distorsionar el resultado. Los resultados se consideran representativos del conjunto en sí, es decir, aplicables al público en general, cuando reflejan la distribución normal en la población.
Si quieres obtener datos de estudios que sean los más fiables posibles, tienes que esforzarte para que tu estudio sea representativo. En la investigación de mercados, necesitas recopilar datos del público objetivo antes de lanzar un producto al mercado, con el fin de ofrecer un producto que los consumidores quieran comprar o utilizar. Sin embargo, no puedes preguntar la opinión de cada comprador potencial, simplemente llevaría demasiado tiempo y no sería rentable. Además, es imposible determinar con exactitud el tamaño del grupo de compradores potenciales. Por tanto, antes de enviar tu estudio a los participantes, tienes que definir un tamaño de muestra que represente a tu público objetivo lo más fielmente posible, y en todas sus facetas.
¿Qué tamaño debe tener una muestra?
Cuanto mayor sea el tamaño de la muestra, más precisos serán los resultados, ¿verdad?
Por lo general, cuanto mayor sea la muestra, más representativa será, siempre que consultemos a las personas adecuadas; es decir, no estudiaremos a los hombres cuando queramos representar a las mujeres embarazadas.
Los resultados de un estudio son considerados representativos cuando reflejan fielmente a la población en general, lo que quiere decir que puedes sacar conclusiones fiables sobre la población general, ya que todas las características de la población objetivo están también presentes en tu muestra.
Así que una muestra más grande facilita alcanzar la representatividad, pero por otro lado, cuanto mayor sea el tamaño de la muestra, mayor coste y tiempo requerirá tu estudio. Entonces, ¿cómo puedes equilibrar costes y representatividad?
Deberás encontrar un equilibrio entre el tamaño de la muestra y el margen de error, es decir, deberás encontrar un tamaño de muestra lo suficientemente grande como para alcanzar el nivel de precisión deseado y mantenerte dentro de un margen de error aceptable.
Echemos un vistazo a la métrica del margen de error y a qué margen de error se considera aceptable.
¿Qué es el margen de error?
El margen de error (o error marginal) es una estadística que expresa el grado de error de muestreo aleatorio en los resultados de un estudio. Cuanto mayor sea el margen de error, menor será la confianza en que el resultado de un estudio refleje con precisión el resultado de un censo de toda la población.
El margen de error se refiere al tamaño de tu muestra y a la diferencia entre los resultados de los datos de tu estudio y los de la distribución poblacional (normal), te indica lo mucho que reflejan tus resultados las opiniones de la población en general.
Veamos un ejemplo.
Como puedes adivinar por la palabra margen, el margen de error es un intervalo de valores en torno a la media muestral.
Por ejemplo, un estudio de 1.000 personas de tu población objetivo te da un margen de error del 5%, lo que significa que el 95% de las veces los resultados están dentro de un margen del 5% de lo que serían si hubieses consultado a cada una de las personas de tu población objetivo. Así, si los datos de tu estudio indican que el 40% de la población total aprueba o desaprueba algo, el margen de error significa que puedes estar seguro en un 95% de que la cifra real se sitúa entre el 35% y el 45%.
El error marginal indica lo cerca que están los resultados de la muestra de la realidad. Puede calcularse teniendo en cuenta el tamaño de la muestra, el margen de error y el nivel de confianza. El error marginal no debe ser demasiado alto, pues de lo contrario puede llevar a conclusiones erróneas que podrían tener graves consecuencias. Un margen de error aceptable utilizado por la mayoría de los investigadores de estudios suele situarse entre el 4% y el 8% con un nivel de confianza del 95%.
Es importante mantener el margen de error lo más bajo posible, ya que cuanto menor sea el margen de error, más confianza podrás tener en tus resultados; cuanto mayor sea el margen de error, más se pueden alejar de las opiniones de la población total, haciendo que tus resultados sean inutilizables.
Como regla general, a medida que aumenta el tamaño de la muestra disminuye el error marginal, pero hay que tener en cuenta que un tamaño de muestra demasiado grande hace que el estudio sea más caro y lleve más tiempo. Por lo tanto, es esencial encontrar un equilibrio entre el error marginal y el tamaño de la muestra. Con una planificación adecuada puedes garantizar que tu muestra sea representativa de la población objetivo, con errores marginales lo más bajos posible para obtener resultados precisos y fiables.
Tengamos en cuenta que lo que se considera un valor aceptable también depende del tipo de investigación que estés realizando. Por razones obvias, los estudios y ensayos médicos tienen normas más estrictas y criterios más rigurosos a la hora de tomar muestras y recopilar resultados que la investigación del comportamiento de compra de los consumidores.
Calculadora de margen de error
Utiliza nuestra calculadora para comprobar rápidamente el margen de error de tu estudio. Sólo tendrás que introducir tus valores y verificar el resultado. Todas las métricas utilizadas en la calculadora se explican detalladamente a continuación. Si tienes alguna otra duda, no dudes en ponerte en contacto con nuestros expertos a través del chat.
Un margen de error aceptable utilizado por la mayoría de los investigadores suele situarse entre el 3% y el 6% con un nivel de confianza del 95%.
Parámetros clave para calcular el tamaño de la muestra y el margen de error
Los valores clave para determinar el tamaño óptimo de la muestra y/o el margen de error son la población total N, la desviación estándar p, el intervalo de confianza (IC) y el valor Z.
Aquí tienes una breve explicación de cada métrica.
Desviación estándar, p
Al examinar los resultados de un estudio, deberías poder hacer afirmaciones generales como "el xx% aprueba esto". Sin embargo, esto puede variar mucho entre los participantes, por lo que también hay que tener en cuenta la desviación estándar.
La desviación estándar se expresa en porcentaje y especifica el rango de respuestas probables para cada pregunta. Cuanto mayor sea este valor, más participantes serán necesarios para obtener un resultado exacto.
El valor de la desviación estándar suele fijarse en 0,5 e indica cuánta variación cabe esperar en las respuestas de los participantes del estudio.
He aquí un ejemplo de cómo puede producirse una desviación estándar elevada al utilizar una pregunta de escala Likert:
Imagina que se realiza un estudio para medir la opinión de las personas sobre un nuevo producto. Una de las preguntas es ¿Cuán probable es que recomiendes este producto a un amigo? Los participantes del estudio responden mediante una pregunta de escala Likert con cinco opciones: "Muy improbable", "Improbable", "Neutral", "Probable", "Muy probable".
De 100 participantes, 50 de ellos eligen "Muy improbable" y los otros 50 eligen "Muy probable". Esto significa que no hay un punto medio en las respuestas, todas están en uno de los dos extremos.
Dado que la mitad de los participantes eligió un extremo y la otra mitad eligió el otro extremo, las respuestas no están distribuidas uniformemente y la desviación estándar sería mucho mayor para indicar la gran diferencia o dispersión entre las respuestas.
Esta elevada desviación estándar es inusual si se compara con una distribución "normal" de respuestas, en la que se esperaría que la mayoría de las respuestas estuvieran cerca de la media, con menos respuestas en los extremos.
Es importante observar que un valor de desviación estándar de 0,5 se considera un valor común y normalmente sólo hay que ajustarlo en casos extremos, como el mencionado en este ejemplo.
Si tienes en mente un caso de uso específico y no estás seguro de qué tipo de desviación estándar esperar, también puedes ponerte en contacto con nuestros expertos para que te asesoren.
Valor Z e intervalo de confianza (IC)
El valor Z mide lo bien que la muestra representa a la población total (incluido el margen de error) y describe la desviación de un valor respecto a la media de tu muestra. O dicho de otro modo: El valor Z indica hasta qué punto puedes asegurar que los resultados de tu estudio se ajustan a la realidad.
Por ser más tangibles, los intervalos de confianza que representan un valor z determinado se suelen utilizar para calcular un tamaño de muestra deseado o un margen de error. Esta tabla muestra los valores Z de los intervalos de confianza más habituales.
| Intervalo de confianza | Valor Z |
| 80% | 1,28 |
| 85% | 1,44 |
| 90% | 1,65 |
| 95% | 1,96 |
| 99% | 2,58 |
Un intervalo de confianza es un rango de valores, derivados de una muestra, que se utiliza para estimar un parámetro poblacional desconocido. Proporciona un nivel de certeza o confianza en que el verdadero parámetro poblacional se encuentra dentro del intervalo.
El intervalo se calcula tomando una estadística muestral (como la media o la proporción) y sumando y restando un margen de error, que viene determinado por el nivel de confianza deseado y el tamaño de la muestra. El nivel de confianza suele expresarse en porcentaje, como 90%, 95% o 99%.
El intervalo de confianza es el rango de valores entre los que esperas que se sitúe tu estimación si vuelves a hacer la prueba, dentro de un determinado nivel de confianza.
Tomemos un ejemplo visual utilizando una distribución normal.
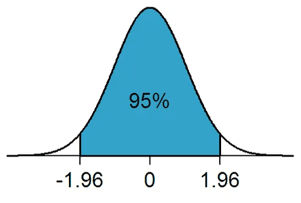
Por ejemplo, la probabilidad de que el valor medio poblacional esté entre -1,96 y +1,96 desviaciones estándar (valores z) de la media muestral es del 95%.
En consecuencia, hay un 5% de probabilidades de que la media de la población quede fuera del intervalo de confianza superior e inferior (como ilustra el 2,5% de valores atípicos a ambos lados de los valores z de 1,96).
Población total, N
En la mayoría de los usos cotidianos, la palabra población implica un grupo de personas o, por lo menos, un grupo de seres vivos. Sin embargo, los especialistas en estadística y los investigadores se refieren al grupo que estudian como población.
La población de un estudio pueden ser madres de niños menores de 5 años, médicos o usuarios de un producto concreto.
Para extraer las conclusiones más precisas posibles, los especialistas en estadística e investigadores necesitarían conocer todas las características de las personas de la población deseada, pero esto es imposible o poco práctico la mayoría de las veces, ya que los conjuntos de población suelen ser bastante grandes.
Por ello, seleccionan muestras de la población, es decir, un grupo más pequeño extraído de la población total que tiene las características de toda la población, de modo que las observaciones y conclusiones realizadas a partir de los datos de la muestra puedan atribuirse a la población en su conjunto.
En la calculadora de Appinio no tenemos en cuenta la población total, ya que en la mayoría de los estudios el tamaño de la población es tan grande (p. ej. todos los españoles) que no afecta al tamaño de la muestra necesaria ni al margen de error. Sólo cuando la población que quieres investigar es extremadamente pequeña -como todos los odontólogos de sexo masculino de Barcelona- es necesario tener en cuenta la población total. En este caso, puedes consultar nuestra fórmula avanzada a continuación o consultar directamente a nuestros expertos para que te orienten.
El caso de la población desconocida
En la mayoría de los casos, no es posible determinar con precisión el tamaño de la población, porque es demasiado amplia y extensa. En estos casos, sólo puedes utilizar la parte superior de la fórmula estándar para calcular el tamaño mínimo de la muestra:
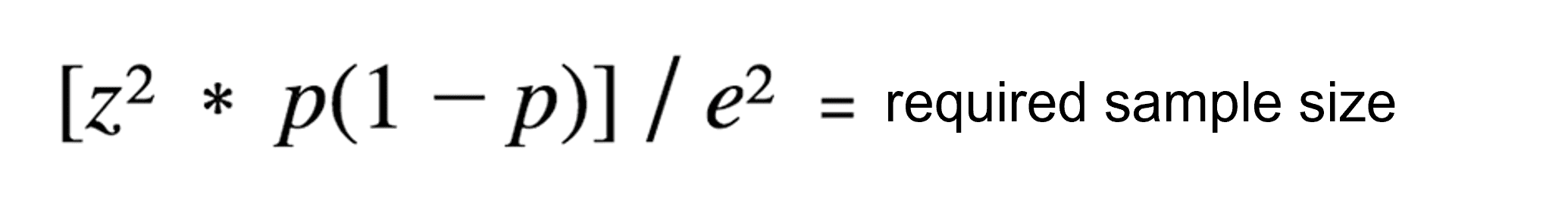
Fórmula para determinar el tamaño de la muestra
Para complementar, también vamos a mostrarte cómo puedes calcular el tamaño adecuado de la muestra utilizando la fórmula ampliada, pero si no te gustan las matemáticas y las fórmulas te traen recuerdos escolares que te gustaría mantener en el pasado, utiliza las calculadoras de Appinio mostradas anteriormente.
Una vez que determines todos los parámetros clave mencionados anteriormente, puedes utilizar la siguiente ecuación para determinar el tamaño óptimo de la muestra. La siguiente fórmula estándar es la más adecuada para tamaños de población pequeños o medianos.
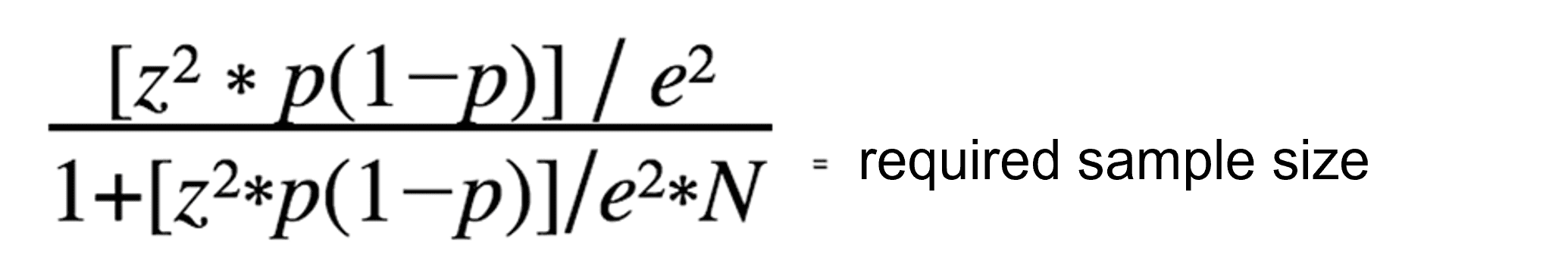Un ejemplo de cálculo: Partimos de una población total N = 500, un margen de error de 0,1, una desviación estándar p de 0,5 y un valor Z de 1,96 (basado en un nivel de confianza del 95%). Entonces se obtiene el siguiente cálculo:
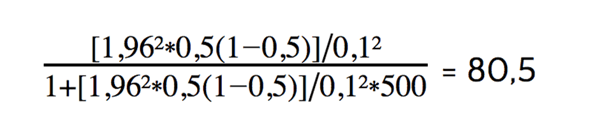Para que los resultados sean representativos de una población total de 500 participantes, el tamaño óptimo de la muestra es de al menos 80 participantes.
Conclusiones
En conclusión, un tamaño de muestra fiable es fundamental para llegar a conclusiones precisas, representativas y significativas al realizar una investigación con estudios. Esto garantiza la minimización de los errores marginales y que los resultados puedan extrapolarse de la población con mayor certeza. Siguiendo la fórmula descrita, puedes determinar el tamaño óptimo de la muestra de tu estudio para garantizar unos resultados precisos y fiables.
Hemos hablado del error marginal, el tamaño de la muestra y el cálculo del valor Z. Para determinar el tamaño de la muestra de un estudio, debes utilizar la fórmula estándar y tener en cuenta tres valores clave: el margen de error, la desviación estándar y el valor Z. En casos concretos en los que quieras representar a una población muy pequeña, hay que considerar adicionalmente el tamaño de la población.
Siguiendo esta fórmula, puedes garantizar la precisión y fiabilidad de los resultados de tu estudio. El error marginal es una medida utilizada para describir lo bien que una muestra representa a la población total y alude a la probabilidad de que se produzca un error. El valor Z se calcula en función del nivel de confianza e indica la seguridad que puedes tener de que tus resultados se ajustan a la realidad. Por último, el tamaño de la muestra debe determinarse utilizando la fórmula estándar para minimizar los errores marginales y extrapolar los resultados a toda la población con precisión.
¿Quieres lanzar tu propio estudio pero no sabes muy bien cómo?
¡Echa un vistazo al Carrusel de insights de Appinio!
Para el Appinio Hype Train consultamos a una población representativa según la edad y el sexo.
Puedes acceder a todos los volúmenes del Carrusel de insights que publicamos en 2022 y registrarte gratuitamente en el dashboard aquí:
