Appinio Research · 25.09.2023 · 19min Temps de lecture
Qu'il s'agisse de questions politiques, de satisfaction client ou d'enquêtes internes auprès d'employés, les études de marché sont le moyen le plus courant de comprendre les tendances, sentiments, croyances et opinions d'un groupe donné. Plus vous posez de questions à un grand nombre de personnes, plus vous vous rapprochez d'un résultat représentatif. Cependant, interroger tous les habitants de France pour connaître leurs intention de vote aux prochaines élections serait un vrai casse-tête, n'est-ce pas ?
C'est là que les échantillons représentatifs entrent en jeu.
Un échantillon représentatif vise à refléter les opinions du grand public en se concentrant sur une partie de la population. Dans le cadre d'une enquête, il est essentiel de déterminer le nombre de participants nécessaire afin d'obtenir un échantillon représentatif. Dans cet article, nous vous présenterons les valeurs clés à prendre en considération pour calculer l'échantillon optimal de votre étude et ainsi garantir des résultats qui reflètent fidèlement votre population.
Vous souhaitez déterminer rapidement la taille de l'échantillon pour votre étude ? Tirez parti de notre calculateur de taille d'échantillon en ligne pour obtenir avec précision l'échantillon nécessaire à votre recherche.
Calculateur de taille d'échantillon
Utilisez notre calculateur pour vérifier rapidement la taille de l'échantillon nécéssaire à votre étude. Il vous suffit d'insérer les valeurs désirées puis de consulter le résultat. Tous les paramètres du calculateur sont minutieusement expliqués dans cet article. Pour toutes questions supplémentaires, nos experts sont à votre disposition via le chat.
Définition : qu'est-ce qu'un échantillon ?
Un échantillon est une petite partie d'une population destinée à représenter l'ensemble de cette dernière. Dans le domaine de la recherche, l'échantillonnage joue un rôle crucial en nous permettant de comprendre une population à travers un prisme plus restreint.
Il existe plusieurs méthodes d'échantillonnage. Vous pouvez par exemple opter pour un échantillon aléatoire, dans lequel chaque individu au sein de la population a une chance équitable d'être choisi pour participer à l'étude.
Un échantillon aléatoire peut être utile pour mener une étude de marché préliminaire ou pour recueillir de nouvelles idées. Toutefois, si vous souhaitez par exemple déterminer avec précision le nombre de Français végétariens, l'utilisation d'un échantillon aléatoire peut poser quelques problèmes. Il est possible que certaines catégories de participants soient sous-représentées dans l'échantillon (par exemple, les femmes), tandis que d'autres groupes peuvent être surreprésentés (par exemple, les Millennials). Par conséquent, les informations obtenues à partir de l'échantillon pourraient ne pas être généralisables à la population cible, limitant ainsi la validité de l'étude.
Pourquoi la taille de l'échantillon est-elle si importante ?
Dans le domaine des études de marché en particulier, il est essentiel que votre échantillon réponde à des critères spécifiques et contienne tous les différents groupes - tels que les femmes, les hommes ou les différentes tranches d'âge - dans les mêmes proportions que la population que vous souhaitez représenter. De plus, la taille de l'échantillon doit être suffisante pour être représentative et ainsi permettre des conclusions fiables.
Il est important de tester la fiabilité de l'échantillon choisi. Si l'échantillon est trop petit, les informations recueillies risquent d'être biaisées ; si l'échantillon est trop grand, vous risquez de gaspiller des ressources, du temps et de l'argent. Les résultats sont considérés comme représentatifs de l'ensemble de la population, c'est-à-dire applicables au grand public, lorsqu'ils reflètent la distribution (normale) de la population.
Afin de garantir la fiabilité des données d'enquête, il est crucial de rendre votre étude représentative. Vous pourrez ainsi comprendre les besoins de votre public cible, et par exemple développer un produit qui répondra parfaitement à leurs attentes. Il est cependant impossible de demander l'avis de chaque acheteur potentiel. Par conséquent, avant d'envoyer votre enquête à vos répondants, vous devez définir une taille d'échantillon qui représente votre population cible aussi fidèlement que possible, sous toutes ses facettes. De cette façon, vous pouvez obtenir des données fiables et applicables à l'ensemble de la population.
Quelle doit être la taille de l'échantillon ?
Comme nous l'avons déjà souligné, la taille de l'échantillon a un impact direct sur la précision et la représentativité des résultats. Il est donc crucial de sélectionner soigneusement les personnes interrogées afin d'obtenir des données qui reflètent de manière adéquate la population cible. Par exemple, il serait contreproductif de questionner des hommes si l'on souhaite obtenir des informations représentatives des femmes enceintes.
Afin de garantir la représentativité de l'enquête, il est essentiel que toutes les caractéristiques de la population ciblée soient présentes dans l'échantillon. Cette condition est indispensable pour obtenir des résultats fiables et tirer des conclusions pertinentes sur l'ensemble de la population.
Un échantillon plus important permet d'augmenter la représentativité des résultats. Cependant, il est important de trouver un équilibre entre la taille de l'échantillon, les coûts et la durée de l'enquête. Il est donc primordial de prendre des décisions judicieuses concernant la taille de l'échantillon et la marge d'erreur. Il est nécessaire de déterminer une taille d'échantillon suffisante pour atteindre le niveau de précision désiré, tout en respectant une marge d'erreur acceptable.
Qu'est-ce que la marge d'erreur ?
La marge d'erreur est une mesure statistique qui exprime la quantité d'erreur due à l'échantillonnage aléatoire dans les résultats d'un sondage. Plus la marge d'erreur est élevée, moins il est probable que le résultat du sondage reflète de manière précise le résultat d'un recensement de l'ensemble de la population, ce qui diminue la confiance que l'on peut accorder aux résultats du sondage. La marge d'erreur dépend de la taille de l'échantillon ainsi que de la différence entre les résultats de l'enquête et ceux de la distribution normale de la population. En d'autres termes, elle permet de mesurer dans quelle mesure les résultats du sondage représentent les opinions de la population dans son ensemble.
Comme son nom l'indique, la marge d'erreur est un intervalle de valeurs situé autour de la moyenne de l'échantillon.
Prenons un exemple :
Si vous menez une enquête auprès de 1 000 personnes de votre population cible et que vous obtenez une marge d'erreur de 5 %, cela signifie que dans 95 % des cas, les résultats se situent dans une fourchette de 5 % de ce qu'ils seraient si vous aviez interrogé chaque personne de votre population cible individuellement. Ainsi, si les données de votre enquête indiquent que 40 % de la population totale approuve ou désapprouve quelque chose, la marge d'erreur vous permet d'être sûr à 95 % que le chiffre réel se situe entre 35 % et 45 %. En somme, la marge d'erreur vous donne une idée de l'exactitude de vos résultats et vous aide à évaluer leur fiabilité.
L'erreur marginale permet de mesurer la proximité des résultats de l'échantillon avec la réalité. Elle est calculée en prenant en compte la taille de l'échantillon, la marge d'erreur et le niveau de confiance. Il est important de maintenir une faible marge d'erreur pour éviter de tirer des conclusions inexactes qui pourraient avoir des répercussions significatives. Une marge d'erreur acceptable, utilisée par la plupart des spécialistes, se situe généralement entre 4 et 8 % à un niveau de confiance de 95 %.
Ainsi plus la marge d'erreur est petite, plus vous pouvez être confiant dans la précision de vos résultats. En revanche, si la marge d'erreur est élevée, les résultats risquent de s'éloigner des opinions de la population totale, ce qui les rendra inutilisables.
En général, la taille de l'échantillon et l'erreur marginale sont inversement proportionnelles : plus la taille de l'échantillon est grande, plus l'erreur marginale est faible. Toutefois, il est important de garder à l'esprit que des échantillons trop grands peuvent rendre l'enquête plus coûteuse et plus longue. Il est donc crucial de trouver un juste milieu entre l'erreur marginale et la taille de l'échantillon. En anticipant soigneusement votre échantillon en amont, vous pouvez vous assurer qu'il soit représentatif de votre population cible, avec une marge d'erreur aussi faible que possible, afin d'obtenir des résultats précis et fiables.
Il ne faut pas oublier que les normes et les critères acceptables varient en fonction du type de recherche que vous menez. Les études et essais médicaux, par exemple, ont des exigences plus rigoureuses en matière d'échantillonnage et de collecte de résultats en raison de leur importance cruciale. Cependant, les recherches sur le comportement d'achat des consommateurs peuvent être moins exigeantes en termes de normes et de critères, car les conséquences des erreurs sont moins graves.
Calculateur de marge d'erreur
Utilisez notre calculateur pour vérifier rapidement la marge d'erreur de votre étude. Il suffit d'entrer vos valeurs et de vérifier le résultat. Tous les paramètres utilisés dans le calculateur sont expliqués en détail ci-dessous. Si vous avez d'autres questions, n'hésitez pas à contacter nos experts via le chat.
Les valeurs clés pour calculer la taille de l'échantillon et la marge d'erreur
Les valeurs clés permettant de déterminer la taille optimale de l'échantillon et/ou la marge d'erreur sont la population totale N, l'écart-type p, l'intervalle de confiance (IC) et le score Z .
Voici une brève explication de chaque mesure.
Écart-type, p
Lors de l'analyse des résultats d'une enquête, il est important d'être en mesure de formuler des déclarations générales, telles que "xx% des participants ont approuvé cela". Cependant, il convient de noter que ce pourcentage peut varier considérablement d'un participant à l'autre, d'où la nécessité de prendre en compte l'écart-type.
L'écart-type, exprimé en pourcentage, précise la plage de réponses probables pour chaque question posée. Si cette valeur est élevée, il faut davantage de participants pour obtenir des résultats précis.
En général, la valeur de l'écart-type est fixée à 0,5 et indique l'ampleur de la variation attendue dans les réponses des personnes interrogées.
Voici un exemple qui illustre comment l'utilisation d'une échelle de Likert peut conduire à un écart-type élevé :
Supposons qu'une enquête soit menée pour mesurer l'opinion des personnes sur un nouveau produit. L'une des questions posées est : "Quelle est la probabilité que vous recommandiez ce produit à un ami ?" Les répondants doivent choisir parmi cinq options de l'échelle de Likert : "Fortement improbable", "Peu probable", "Neutre", "Probable", "Fortement probable".
Sur les 100 personnes interrogées, 50 répondent "Très improbable" et les 50 autres répondent "Très probable". Cela signifie que toutes les réponses sont soit à l'un des deux extrêmes, sans de réponse intermédiaire.
Comme les réponses de la moitié des participants se regroupent autour d'un extrême de l'échelle de Likert et l'autre moitié autour de l'autre extrême, la distribution des réponses n'est pas uniforme, ce qui entraîne un écart-type beaucoup plus élevé pour indiquer l'importante différence ou l'écart entre les réponses.
Un écart-type élevé comme celui-ci est atypique par rapport à une distribution « normale » des réponses, où l'on s'attendrait à ce que la majorité des réponses se regroupent autour de la moyenne, avec moins de réponses aux extrêmes.
Il est à noter que la valeur courante de l'écart-type est de 0,5 et qu'il ne doit généralement être ajusté que dans les cas extrêmes, comme celui mentionné dans cet exemple.
Si vous avez un cas particulier en tête et que vous n'êtes pas certain du type d'écart-type à prévoir, vous pouvez également contacter nos experts pour obtenir de l'aide.
Score Z, z, et intervalle de confiance (IC)
Le score Z est une mesure qui permet d'évaluer la représentativité de votre échantillon par rapport à la population totale, en tenant compte de la marge d'erreur. Il décrit également l'écart entre une valeur et la moyenne de l'échantillon. En d'autres termes, le score Z indique dans quelle mesure les résultats de votre étude reflètent la réalité.
Les intervalles de confiance, qui sont associés à un score Z spécifique, sont couramment utilisés pour déterminer la taille d'un échantillon ou la marge d'erreur souhaitée. Le tableau ci-dessous présente les scores Z les plus couramment utilisés pour les intervalles de confiance.
| Confidence Interval | Z-value |
| 80% | 1,28 |
| 85% | 1,44 |
| 90% | 1,65 |
| 95% | 1,96 |
| 99% | 2,58 |
Un intervalle de confiance est une plage de valeurs dérivée d'un échantillon, qui permet d'estimer un paramètre de population inconnue avec un certain niveau de certitude ou de confiance. Pour le calculer, on utilise une statistique d'échantillon (telle que la moyenne ou la proportion) à laquelle on ajoute et soustrait une marge d'erreur. Cette dernière est déterminée par le niveau de confiance souhaité et la taille de l'échantillon, et est généralement exprimée en pourcentage (par exemple, 90%, 95% ou 99%).
L'intervalle de confiance représente la fourchette de valeurs entre lesquelles on peut raisonnablement estimer que se situera la vraie valeur du paramètre de population, si l'on répétait le test plusieurs fois avec le même échantillon et le même niveau de confiance.
Prenons un exemple visuel en utilisant une distribution normale.
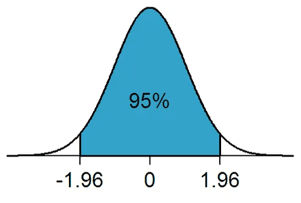
Par exemple, la probabilité que la valeur moyenne de la population se situe entre -1,96 et +1,96 écart-type (z-score) par rapport à la moyenne de l'échantillon est de 95 %.
Par conséquent, il y a 5 % de chances que la moyenne de la population se situe en dehors de l'intervalle de confiance supérieur et inférieur (comme l'illustrent les extrêmes de 2,5 % de part et d'autre des z-scores de 1,96).
Total population, N
Dans le langage courant, le terme "population" se réfère généralement à un groupe de personnes ou d'êtres vivants. Cependant, en statistique et en recherche, ce terme désigne le groupe étudié.
La population étudiée peut être composée de mères d'enfants de moins de 5 ans, de médecins ou d'utilisateurs d'un produit spécifique, par exemple.
Pour tirer des conclusions précises, les statisticiens et les chercheurs devraient idéalement connaître toutes les caractéristiques des personnes appartenant à la population étudiée. Cependant, dans la plupart des cas, cela est impossible et/ou peu pratique en raison de la taille souvent importante des populations.
C'est pourquoi les statisticiens choisissent généralement un échantillon, c'est à dire un groupe plus petit représentatif de la population totale, pour obtenir des données qui peuvent être généralisées à l'ensemble de la population.
Dans notre calculateur Appinio, nous n'avons pas besoin de considérer la taille de la population totale car, pour la plupart des études, la taille de la population est si importante (par exemple, tous les Français) qu'elle n'affecte pas la taille de l'échantillon requis ou la marge d'erreur. Ce n'est que pour les populations extrêmement restreintes, comme tous les dentistes masculins de Londres par exemple, que la taille de la population doit être prise en compte. Dans ce cas, vous pouvez vous référer à notre formule avancée ci-dessous ou contacter directement nos experts pour obtenir de l'aide.
Cas d'une population inconnue
Dans la plupart des cas, il est impossible de déterminer précisément la taille de la population, car elle est trop grande et trop vaste. Dans ce cas, seule la partie supérieure de la formule standard peut être utilisée pour calculer la taille minimale de l'échantillon :
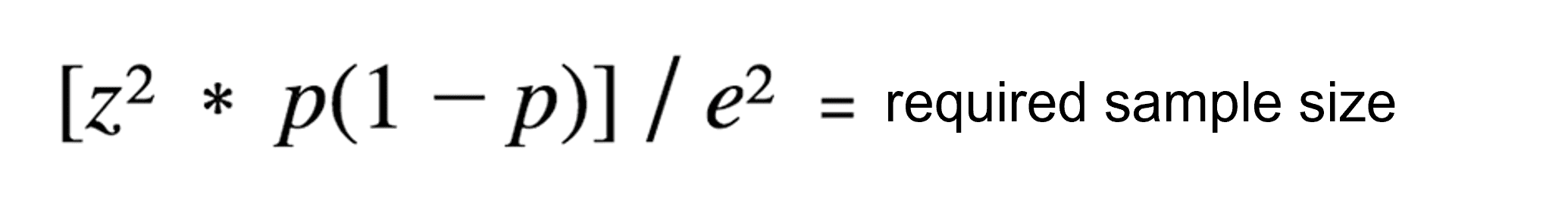
Formule pour déterminer la taille de l'échantillon
Par souci d'exhaustivité, nous allons également vous montrer comment calculer la taille appropriée de l'échantillon à l'aide de la formule étendue. Toutefois, si vous préférez éviter les calculs mathématiques ou si les formules vous rappellent des souvenirs d'école que vous préférez oublier, vous pouvez utiliser nos calculateurs Appinio ci-dessus.
Une fois que vous avez déterminé toutes les valeurs clés mentionnées précédemment, vous pouvez utiliser l'équation ci-dessous pour déterminer la taille optimale de l'échantillon. Cependant, notez que la formule standard suivante convient mieux aux populations de taille petite à moyenne.
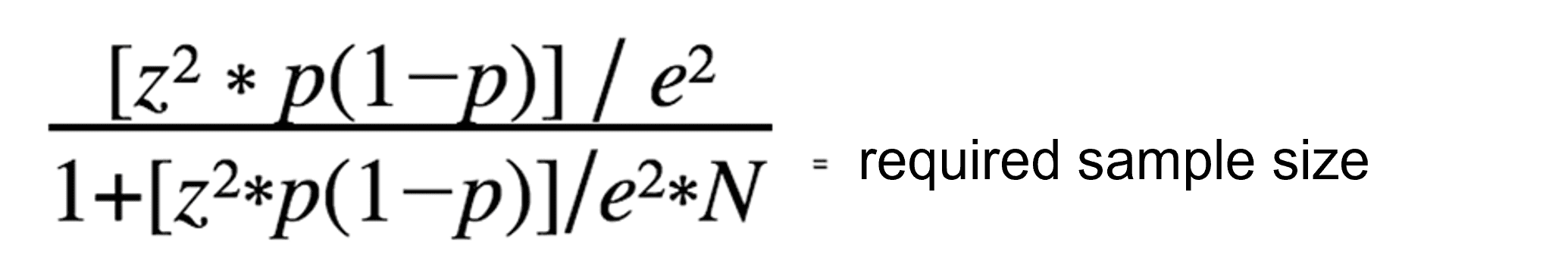Exemple de calcul : Le point de départ est une population totale N = 500, une marge d'erreur de 0,1, un écart-type p de 0,5 et un score Z de 1,96 (sur la base d'un niveau de confiance de 95 %). Le calcul suivant est alors effectué :
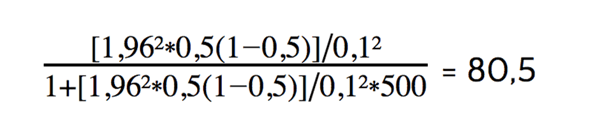Pour que les résultats soient représentatifs d'une population totale de 500 répondants, la taille optimale de l'échantillon est d'au moins 80 répondants.
Conclusions
En conclusion, une taille d'échantillon fiable est essentielle pour tirer des conclusions précises, représentatives et significatives lors de la réalisation d'une enquête. Cela permet de minimiser les erreurs marginales et d'extrapoler les résultats à partir de la population avec une plus grande certitude. En suivant la formule décrite, vous pouvez déterminer la taille optimale de l'échantillon pour votre étude afin de garantir des résultats précis et fiables.
Nous avons discuté de l'erreur marginale, de la taille de l'échantillon et du calcul du score Z. Pour déterminer la taille de l'échantillon d'une enquête, vous devez utiliser la formule standard et tenir compte de trois valeurs clés : la marge d'erreur, l'écart-type et le score Z. Dans des cas particuliers, notamment lorsque vous voulez représenter une population très restreinte, la taille de la population doit également être prise en compte.
En suivant cette formule, vous pouvez garantir la précision et la fiabilité des résultats de votre enquête. L'erreur marginale est une mesure utilisée pour évaluer la représentativité de l'échantillon par rapport à la population totale et se réfère à la probabilité qu'une erreur se produise. La valeur Z est calculée sur la base du niveau de confiance et indique dans quelle mesure vous pouvez être certain que vos résultats correspondent à la réalité. Enfin, la taille de l'échantillon doit être déterminée à l'aide de la formule standard afin de minimiser les erreurs marginales et d'extrapoler les résultats à l'ensemble de la population avec précision.
Vous voulez lancer une enquête, mais ne savez pas où commencer ?
Jetez un coup d'œil à notre plateforme ! Nous publions régulièrement des études représentatives en termes d'âge, de genre, de région et de catégorie socio-professionnelle.
Pour découvrir la plateforme Appinio et explorer nos études publiques, c'est par ici :
