Appinio Research · 06.03.2023 · 16min Lesezeit
Ob es um die politische Meinung, die Kundenzufriedenheit, den Appinio Hype Train oder eine Mitarbeiterbefragung in einem Unternehmen geht, Umfragen sind das gängigste Mittel, um die öffentliche Stimmung, Meinungen, Überzeugungen und Tendenzen zu ermitteln. Und je mehr Menschen man befragt, desto näher kommt man natürlich an ein repräsentatives Ergebnis heran. Aber stellen Sie sich vor, Sie würden alle Menschen im Vereinigten Königreich befragen, um herauszufinden, wen sie bei der nächsten Wahl wählen würden - unmöglich!
An dieser Stelle kommt die Notwendigkeit einer repräsentativen Stichprobe ins Spiel.
Eine repräsentative Stichprobe konzentriert sich auf einen Teil der Bevölkerung und zielt darauf ab, die Ansichten der Allgemeinheit widerzuspiegeln. Aber woher weiß man, insbesondere in der Umfrageforschung, wie viele Befragte man benötigt, um eine repräsentative Stichprobe der Bevölkerung zu erhalten? Welche Variablen müssen Sie berücksichtigen? In diesem Artikel zeigen wir Ihnen, welche Schlüsselwerte Sie benötigen, um die perfekte Stichprobe für Ihre Studie zu berechnen und wie genau Ihre Ergebnisse die Bevölkerung repräsentieren.
Sie wollen den Stichprobenumfang für Ihre Studie schnell berechnen und haben bereits alle Eckwerte? Dann nutzen Sie unseren Online-Stichprobenberechner, um die benötigte Stichprobe zu ermitteln.
Stichproben-Rechner
Nutzen Sie unseren Rechner, um die Stichprobengröße für Ihre Studie schnell zu ermitteln. Geben Sie einfach Ihre Werte ein und prüfen Sie das Ergebnis. Alle im Rechner verwendeten Metriken werden im weiteren Verlauf des Artikels ausführlich erläutert. Wenn Sie weitere Fragen haben, können Sie sich gerne über den Chat an unsere Experten wenden.
Definition: Was ist eine Stichprobe?
Eine Stichprobe ist ein kleiner Teil oder eine kleine Menge, die zeigen soll, wie die Gesamtheit ist.
Es gibt verschiedene Methoden der Stichprobenerhebung, z.B. eine "Zufallsstichprobe", bei der die Befragten rein zufällig aus der Gesamtbevölkerung ausgewählt werden, so dass jedes Mitglied der Gesamtbevölkerung die gleiche Chance hat, für die Studie ausgewählt zu werden.
Eine Zufallsstichprobe ist nützlich, wenn Sie explorative Marktforschung betreiben oder neue Ideen sammeln wollen, aber sie wäre nicht sinnvoll, wenn Sie wissen wollen, wie viele Briten Veganer sind, da Ihre Zufallsstichprobe einige Teilnehmer ausschließen könnte (z.B., nicht genügend Frauen) oder zu viele Personen aus derselben Gruppe einschließen könnte (z.B., zu viele Millennials), so dass Sie nicht in der Lage wären, Erkenntnisse zu gewinnen, die auf Ihre gewünschte Zielgruppe oder die allgemeine Bevölkerung anwendbar sind.
Warum die Stichprobengröße wichtig ist
Gerade in der Umfrageforschung muss eine Stichprobe bestimmte Kriterien erfüllen und alle verschiedenen Gruppen - wie Frauen, Männer oder verschiedene Altersgruppen - im gleichen Verhältnis zur Gesamtbevölkerung enthalten. Außerdem sollte die Stichprobe groß genug sein, um nicht nur repräsentativ zu sein, sondern auch zuverlässige Aussagen zu machen. Bei der Auswahl einer Stichprobe ist es wichtig, ihre Zuverlässigkeit zu prüfen. Ist die Stichprobe zu klein, können die gesammelten Informationen unvollständig sein, ist die Stichprobe hingegen zu groß, wäre dies eine Verschwendung von Ressourcen. Je größer die Gruppe ist, desto näher liegen die Ergebnisse am Zielmarkt, desto weniger Zufallsfaktoren, Fehler und falsche Aussagen können das Ergebnis verzerren. Die Ergebnisse gelten als repräsentativ für die Gesamtheit, d. h. für die Allgemeinheit, wenn sie die Normalverteilung in der Population widerspiegeln.
Wenn Sie möglichst zuverlässige Umfragedaten erhalten wollen, müssen Sie sich bemühen, Ihre Umfrage repräsentativ zu gestalten. In der Marktforschung müssen Sie Daten von der Zielgruppe sammeln, bevor Sie ein Produkt auf den Markt bringen, damit Sie ein Produkt anbieten können, das die Verbraucher auch kaufen oder benutzen wollen. Sie können jedoch nicht jeden potenziellen Käufer nach seiner Meinung fragen, das wäre einfach zu zeitaufwändig und nicht kosteneffizient. Außerdem ist es unmöglich, die Größe der potenziellen Käufergruppe genau zu bestimmen. Daher müssen Sie, bevor Sie Ihre Umfrage an die Befragten verschicken, eine Stichprobengröße festlegen, die Ihre Zielpopulation so gut wie möglich und in all ihren Facetten repräsentiert.
Wie groß sollte eine Stichprobe sein?
Je größer die Stichprobe ist, desto genauer sind die Ergebnisse, richtig?
Im Allgemeinen gilt: Je größer die Stichprobe, desto repräsentativer ist sie.
Die Ergebnisse einer Umfrage gelten als repräsentativ, wenn die Ergebnisse der Umfrage die Gesamtbevölkerung genau widerspiegeln, was bedeutet, dass Sie zuverlässige Schlussfolgerungen über die allgemeine Bevölkerung ziehen können, da alle Merkmale der Zielbevölkerung auch in Ihrer Stichprobe vorhanden sind.
Mit einer größeren Stichprobe ist es also einfacher, Repräsentativität zu erreichen, aber andererseits ist die Erhebung umso teurer und zeitaufwändiger, je größer die Stichprobe ist. Wie können Sie also Kosten und Repräsentativität in Einklang bringen?
Dazu müssen Sie einen Kompromiss zwischen der Größe der Stichprobe und der Fehlermarge eingehen, d. h. Sie müssen eine Stichprobengröße finden, die groß genug ist, um das gewünschte Präzisionsniveau zu erreichen und innerhalb einer akzeptablen Fehlermarge zu bleiben.
Werfen wir einen Blick auf die Fehlerspannungsmetrik und darauf, welche Fehlerspanne als akzeptabel angesehen wird.
Was ist die Fehlermarge?
Die Fehlermarge (oder der marginale Fehler) ist eine Statistik, die den Umfang des Stichprobenfehlers in den Ergebnissen einer Umfrage angibt. Je größer die Fehlermarge ist, desto weniger Vertrauen sollte man haben, dass ein Umfrageergebnis das Ergebnis einer Volkszählung der gesamten Bevölkerung widerspiegelt.
Die Fehlermarge bezieht sich auf die Größe Ihrer Stichprobe und die Differenz zwischen den Ergebnissen Ihrer Umfragedaten und denen der Gesamtbevölkerung (Normalverteilung); sie gibt an, wie nahe Ihre Ergebnisse den Ansichten der Gesamtbevölkerung kommen.
Nehmen wir ein Beispiel.
Wie das Wort Marge schon sagt, handelt es sich bei der Fehlermarge um einen Wertebereich um den Stichprobenmittelwert.
Bei einer Umfrage unter 1000 Personen haben Sie beispielsweise eine Fehlermarge von 5 %, d. h. die Ergebnisse liegen in 95 % der Fälle innerhalb eines Bereichs von 5 % dessen, was sie wären, wenn Sie jede einzelne Person Ihrer Zielpopulation befragt hätten. Wenn also aus Ihren Umfragedaten hervorgeht, dass 40 % der Gesamtbevölkerung etwas gutheißen oder ablehnen, bedeutet die Fehlermarge, dass Sie zu 95 % sicher sein können, dass die wahre Zahl zwischen 35 % und 45 % liegt.
Der marginale Fehler gibt an, wie nahe die Ergebnisse der Stichprobe an der Realität liegen. Er kann unter Berücksichtigung des Stichprobenumfangs, der Fehlermarge und des Konfidenzniveaus berechnet werden. Der marginale Fehler sollte nicht zu hoch sein, da er sonst zu falschen Schlussfolgerungen führen kann, die schwerwiegende Folgen haben könnten. Eine akzeptable Fehlermarge, die von den meisten Umfrageforschern verwendet wird, liegt in der Regel zwischen 4 % und 8 % bei einem Konfidenzniveau von 95 %.
Es ist wichtig, die Fehlermarge so gering wie möglich zu halten, denn je kleiner die Fehlermarge ist, desto mehr Vertrauen können Sie in Ihre Ergebnisse haben, je größer die Fehlermarge ist, desto weiter können sie von den Ansichten der Gesamtbevölkerung abweichen, was Ihre Ergebnisse unbrauchbar macht.
Als Faustregel gilt, dass der marginale Fehler mit zunehmender Stichprobengröße abnimmt, doch ist zu beachten, dass eine zu große Stichprobengröße die Erhebung teurer und zeitaufwändiger macht. Daher ist es wichtig, ein Gleichgewicht zwischen dem Grenzfehler und dem Stichprobenumfang zu finden. Mit der richtigen Planung können Sie sicherstellen, dass Ihre Stichprobe repräsentativ für die Zielpopulation ist und der Grenzfehler so gering wie möglich ist, damit Ihre Ergebnisse genau und zuverlässig sind.
Was als akzeptabler Wert gilt, hängt auch von der Art der Forschung ab, die Sie durchführen. Aus offensichtlichen Gründen gelten für medizinische Studien und Versuche höhere Standards und strengere Kriterien für die Stichprobenziehung und die Erfassung der Ergebnisse als für die Erforschung des Kaufverhaltens der Verbraucher.
Rechner für die Fehlermarge
Nutzen Sie unseren Rechner, um die Fehlermarge für Ihre Studie schnell zu überprüfen. Geben Sie einfach Ihre Werte ein und prüfen Sie das Ergebnis. Alle im Rechner verwendeten Metriken werden weiter unten im Detail erklärt. Wenn Sie weitere Fragen haben, können Sie sich gerne über den Chat an unsere Experten wenden.
Eine akzeptable Fehlermarge, die von den meisten Forschern verwendet wird, liegt in der Regel zwischen 3 % und 6 % bei einem Konfidenzniveau von 95 %.
Die Schlüsselwerte zur Berechnung von Stichprobenumfang und Fehlermarge
Die Schlüsselwerte zur Bestimmung des optimalen Stichprobenumfangs und/oder der Fehlermarge sind die Gesamtbevölkerung N, die Standardabweichung p, das Konfidenzintervall (CI) und der Z-Wert z.
Hier eine kurze Erklärung für jede Kennzahl.
Standardabweichung, p
Bei der Betrachtung von Umfrageergebnissen sollten Sie in der Lage sein, allgemeine Aussagen zu treffen, wie z. B. "xx % stimmen dem zu". Dies kann jedoch von Befragten zu Befragten stark variieren, weshalb wir auch die Standardabweichung berücksichtigen müssen.
Die Standardabweichung wird in Prozent ausgedrückt und gibt den Bereich der wahrscheinlichen Antworten für jede Frage an. Je höher dieser Wert ist, desto mehr Teilnehmer werden benötigt, um ein genaues Ergebnis zu erhalten.
Der Wert der Standardabweichung wird in der Regel auf 0,5 festgelegt und gibt an, wie groß die erwartete Streuung bei den Antworten der Befragten ist.
Hier ein Beispiel dafür, wie eine hohe Standardabweichung bei der Verwendung einer Frage mit Likert-Skala auftreten kann:
Stellen Sie sich vor, es wird eine Umfrage durchgeführt, um die Meinung der Menschen über ein neues Produkt zu ermitteln. Eine der Fragen lautet: Wie wahrscheinlich ist es, dass Sie dieses Produkt einem Freund empfehlen? Die Befragten antworten mittels einer Likert-Skala mit fünf Optionen: "Sehr unwahrscheinlich", "Unwahrscheinlich", "Neutral", "Wahrscheinlich", "Sehr wahrscheinlich".
Von 100 Befragten entscheiden sich 50 für "Sehr unwahrscheinlich" und die anderen 50 für "Sehr wahrscheinlich". Das bedeutet, dass es bei den Antworten kein Mittelding gibt, sondern dass sie sich alle auf eines der beiden Extreme beziehen.
Da die Hälfte der Befragten das eine Extrem und die andere Hälfte das andere Extrem wählt, sind die Antworten nicht gleichmäßig verteilt und die Standardabweichung wäre viel höher, um den großen Unterschied oder die Streuung zwischen den Antworten anzuzeigen.
Diese hohe Standardabweichung ist ungewöhnlich, wenn man sie mit einer "normalen" Verteilung der Beantwortungen vergleicht, bei der man erwarten würde, dass die meisten Beantwortungen in der Nähe des Durchschnitts liegen und weniger Beantwortungen an den Extremen.
Es ist wichtig zu beachten, dass eine Standardabweichung von 0,5 ein üblicher Wert ist und in der Regel nur in Grenzfällen, wie dem in diesem Beispiel genannten, angepasst werden muss.
Wenn Sie einen bestimmten Anwendungsfall vor Augen haben und sich nicht sicher sind, welche Art von Standardabweichung zu erwarten ist, können Sie sich auch an unsere Experten wenden, um Unterstützung zu erhalten.
Z-Score, z, und Konfidenzintervall (CI)
Der Z-Wert misst, wie gut die Stichprobe die Gesamtpopulation repräsentiert (einschließlich der Fehlermarge) und beschreibt die Abweichung eines Wertes vom Durchschnitt Ihrer Stichprobe. Oder mit anderen Worten: Der Z-Wert gibt an, wie sicher Sie sein können, dass Ihre Studienergebnisse der Realität entsprechen.
Da er greifbarer ist, werden Konfidenzintervalle, die einen bestimmten z-Wert darstellen, in der Regel zur Berechnung einer gewünschten Stichprobengröße oder Fehlermarge verwendet. Diese Tabelle zeigt die z-Werte für die gebräuchlichsten Konfidenzintervalle.
| Konfidenzintervall | Z-Wert |
| 80% | 1,28 |
| 85% | 1,44 |
| 90% | 1,65 |
| 95% | 1,96 |
| 99% | 2,58 |
Ein Konfidenzintervall ist ein aus einer Stichprobe abgeleiteter Wertebereich, der zur Schätzung eines unbekannten Populationsparameters verwendet wird. Es bietet einen Grad an Sicherheit oder Vertrauen, dass der wahre Populationsparameter innerhalb des Intervalls liegt.
Das Intervall wird berechnet, indem eine Stichprobenstatistik (z. B. der Mittelwert oder der Anteil) genommen und eine Fehlermarge addiert und subtrahiert wird, die durch das gewünschte Konfidenzniveau und den Stichprobenumfang bestimmt wird. Das Konfidenzniveau wird in der Regel als Prozentsatz ausgedrückt, z. B. 90 %, 95 % oder 99 %.
Das Konfidenzintervall ist der Wertebereich, in dem Sie erwarten, dass Ihre Schätzung bei einer Wiederholung des Tests innerhalb eines bestimmten Konfidenzniveaus liegen wird.
Nehmen wir ein anschauliches Beispiel mit einer Normalverteilung:
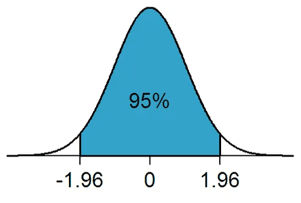
So beträgt beispielsweise die Wahrscheinlichkeit, dass der Mittelwert der Gesamtbevölkerung zwischen -1,96 und +1,96 Standardabweichungen (z-Scores) vom Stichprobenmittelwert liegt, 95 %.
Dementsprechend besteht eine 5 %ige Chance, dass der Mittelwert der Gesamtbevölkerung außerhalb des oberen und unteren Konfidenzintervalls liegt (wie durch die 2,5 % Ausreißer auf beiden Seiten des z-Scores von 1,96 veranschaulicht).
Gesamtbevölkerung, N
Im alltäglichen Sprachgebrauch steht das Wort Bevölkerung meist für eine Gruppe von Menschen oder zumindest für eine Gruppe von Lebewesen. Statistiker und Forscher bezeichnen jedoch jede Gruppe, die sie untersuchen, als Population.
Die Gesamtbevölkerung einer Studie könnten Mütter von Kindern unter 5 Jahren, Ärzte oder Nutzer eines bestimmten Produkts sein.
Um möglichst genaue Schlussfolgerungen ziehen zu können, müssten die Statistiker und Forscher alle Merkmale der Personen in der gewünschten Population kennen, was jedoch in den meisten Fällen unmöglich oder unpraktisch ist, da die Populationen in der Regel recht groß sind.
Deshalb wählen sie Stichproben der Bevölkerung, d. h. eine kleinere Gruppe aus der Gesamtbevölkerung, die die Merkmale der gesamten Bevölkerung aufweist, so dass die Beobachtungen und Schlussfolgerungen, die anhand der Stichprobendaten gemacht werden, auf die Gesamtbevölkerung übertragen werden können.
In unserem Appinio-Rechner berücksichtigen wir nicht die Gesamtbevölkerung, da bei den meisten Studien die Gesamtbevölkerung so groß ist (z. B. alle Deutschen), dass sie keinen Einfluss auf die erforderliche Stichprobengröße oder Fehlermarge hat. Nur wenn die zu untersuchende Population extrem klein ist - wie alle männlichen Zahnärzte in London - muss die Gesamtpopulation berücksichtigt werden. In diesem Fall können Sie sich unsere erweiterte Formel ansehen oder direkt unsere Experten um Hilfe bitten.
Live Chat starten
Der Fall einer unbekannten Population
In den meisten Fällen ist es nicht möglich, den Umfang der Gesamtbevölkerung genau zu bestimmen, da diese zu groß und zu breit ist. In diesen Fällen können Sie nur den oberen Teil der Standardformel zur Berechnung des Mindeststichprobengröße verwenden:
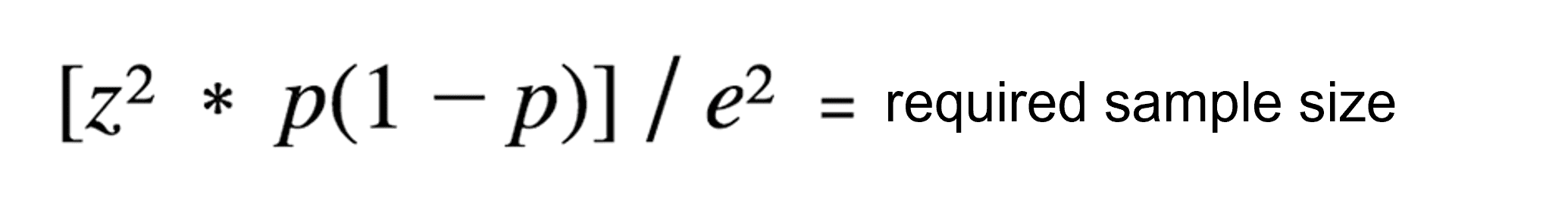
Formel zur Bestimmung der Stichprobengröße
Der Vollständigkeit halber zeigen wir Ihnen auch, wie Sie den angemessenen Stichprobengröße mithilfe der erweiterten Formel berechnen können. Wenn Sie jedoch kein Fan von Mathematik sind und Formeln Erinnerungen an die Schulzeit wecken, die Sie lieber für sich behalten möchten, verwenden Sie unsere obigen Appinio-Rechner.
Sobald Sie alle oben genannten Schlüsselwerte ermittelt haben, können Sie die nachstehende Gleichung zur Bestimmung der optimalen Stichprobengröße verwenden. Die folgende Standardformel ist am besten für kleine bis mittlere Populationsgrößen geeignet.
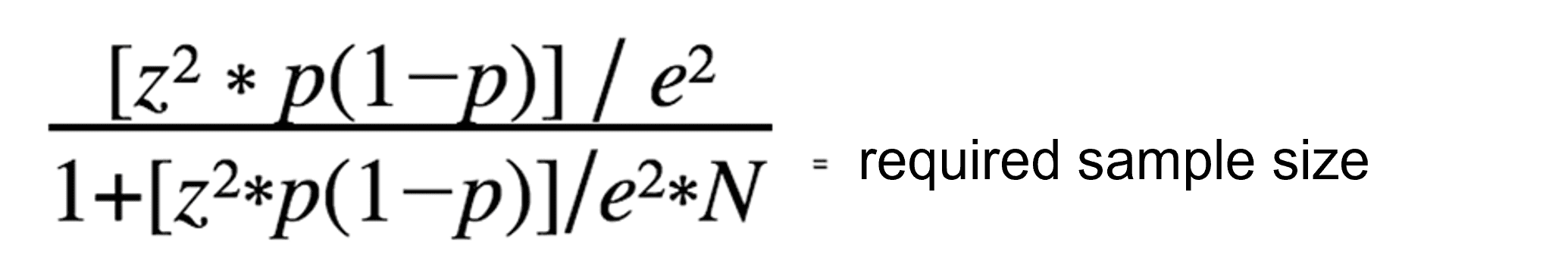Ein Berechnungsbeispiel: Ausgangspunkt ist eine Gesamtpopulation N = 500, eine Fehlermarge von 0,1, eine Standardabweichung p von 0,5 und ein Z-Wert von 1,96 (basierend auf einem Konfidenzniveau von 95%). Dann ergibt sich die folgende Berechnung:
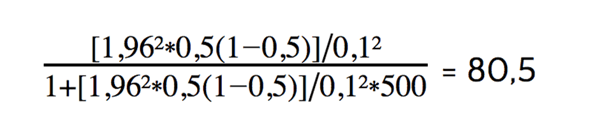Damit die Ergebnisse für eine Gesamtpopulation von 500 Befragten repräsentativ sind, liegt die optimale Stichprobengröße bei mindestens 80 Befragten.
Zusammenfassung
Zusammenfassend lässt sich sagen, dass ein zuverlässiger Stichprobengröße entscheidend ist, um genaue, repräsentative und aussagekräftige Schlussfolgerungen bei der Durchführung von Erhebungen zu ziehen. Dadurch wird sichergestellt, dass marginale Fehler minimiert werden und dass die Ergebnisse mit größerer Sicherheit aus der Gesamtbevölkerung extrapoliert werden können. Anhand der skizzierten Formel können Sie die optimale Stichprobengröße für Ihre Studie ermitteln, um genaue und zuverlässige Ergebnisse zu gewährleisten.
Wir haben den marginalen Fehler, den Stichprobenumfang und die Berechnung des Z-Wertes besprochen. Um den Stichprobenumfang für eine Umfrage zu bestimmen, müssen Sie die Standardformel verwenden und drei Schlüsselwerte berücksichtigen: Irrtumswahrscheinlichkeit, Standardabweichung und Z-Wert. In speziellen Anwendungsfällen, in denen Sie eine sehr kleine Population repräsentieren möchten, muss die Populationsgröße zusätzlich berücksichtigt werden.
Wenn Sie diese Formel befolgen, können Sie die Genauigkeit und Zuverlässigkeit Ihrer Umfrageergebnisse gewährleisten. Der marginale Fehler ist ein Maß, das beschreibt, wie gut eine Stichprobe die Gesamtbevölkerung repräsentiert, und bezieht sich auf die Wahrscheinlichkeit des Auftretens eines Fehlers. Der Z-Wert wird auf der Grundlage des Konfidenzniveaus berechnet und gibt an, wie sicher Sie sein können, dass Ihre Ergebnisse der Realität entsprechen. Schließlich sollte der Stichprobenumfang anhand der Standardformel bestimmt werden, um marginale Fehler zu minimieren und die Ergebnisse genau auf die Gesamtpopulation zu extrapolieren.
Möchten Sie Ihre eigene Umfrage starten, wissen aber nicht genau, wie?
Werfen Sie einen Blick auf den Appinio Hype Tracker Report!
Für die Appinio Hype Tracker Reports untersuchen wir eine nach Alter und Geschlecht repräsentative Grundgesamtheit.
Finden Sie alle Appinio Hype Tracker Bände auf unserer Report Seite und registrieren Sie sich hier kostenlos für das Dashboard.
