What is Stratified Random Sampling? Definition, Method, Examples

Have you ever wondered how researchers obtain accurate and representative data from diverse populations? One powerful tool stands out in the world of research: stratified random sampling. This guide will demystify the complexities, walk you through the intricacies, and equip you with the knowledge and skills to master the art of stratified random sampling.

Whether you're conducting healthcare surveys, market research, environmental studies, or educational research, this guide will be your compass to navigate the terrain of sampling with precision and confidence.

What is Stratified Random Sampling?

Stratified random sampling is a systematic and sophisticated sampling technique used in various research fields to enhance the representativeness and accuracy of collected data. It involves dividing a population into distinct subgroups, or strata, based on specific characteristics or attributes and then selecting samples independently from each stratum.

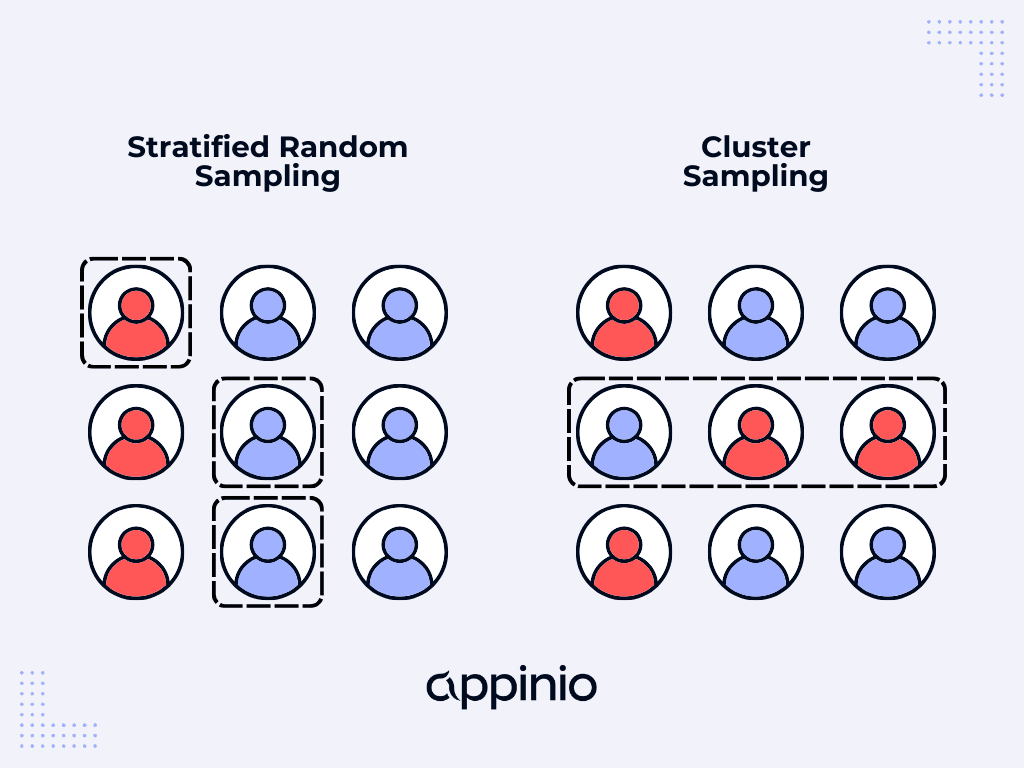
This method serves a dual purpose:

1. Enhancing Precision: By categorizing the population into homogeneous subgroups, stratified random sampling reduces variability within each stratum. This results in more precise estimates and greater statistical power, making it easier to draw meaningful conclusions from the sample.
2. Ensuring Representation: Stratification ensures that all relevant subgroups within a population are adequately represented in the sample. This representation is crucial when studying diverse populations or when certain subgroups are of particular interest due to their unique characteristics or behaviors.

Importance of Stratification

Stratification plays a pivotal role in the success of stratified random sampling. Here are key reasons why stratification is vital:

• Addressing Heterogeneity: Populations are often heterogeneous, with significant variations in characteristics. Stratification allows researchers to account for this diversity by creating subgroups that are more homogeneous, making the data analysis more meaningful.
• Accurate Representation: Stratified random sampling ensures that each stratum is represented proportionally in the sample. This prevents underrepresentation or overrepresentation of specific subgroups, which could bias research findings.
• Effective Subgroup Analysis: When researchers want to make comparisons or draw conclusions about specific subgroups within a population, stratified random sampling provides the necessary foundation. It enables the study of subgroup characteristics, behaviors, or preferences in detail.
• Increased Statistical Power: By reducing variability within strata, stratification enhances the precision of estimates. This increased precision leads to higher statistical power, allowing researchers to detect smaller differences or effects confidently.
• Improved Generalizability: Findings from a stratified random sample are more likely to be generalizable to the entire population because the sample reflects the population's diversity more accurately.

Stratification is not only a statistical technique but also a strategic decision that directly impacts the quality and relevance of research outcomes. When applied thoughtfully, it ensures that research findings are not only robust but also applicable to specific subgroups within a population, contributing to more informed decision-making and valuable insights across various fields of study.

Key Concepts in Stratified Random Sampling

Let's delve deeper into the key concepts that underpin stratified random sampling, providing you with a more comprehensive understanding of these critical elements.

Population

The concept of population is at the core of all sampling methods. It represents the entire group or collection of individuals, items, or entities you aim to study or draw conclusions about. Your research findings will be based on your sample, but the population is the broader context from which you want to generalize your results.

When defining your population, be specific about its boundaries and characteristics. The precision of your research question and objectives will guide your population definition.

Sampling Frame

A robust and well-constructed sampling frame is vital to the success of your stratified random sampling process. It serves as the source or list from which you will draw your sample. The ideal sampling frame should encompass all the members or elements of your target population.

Imagine you're conducting a survey of college students. Your sampling frame would ideally include the names or identities of every student currently enrolled in the college. A comprehensive and accurate sampling frame is crucial to avoid bias in your sample.

Strata

Strata are the building blocks of stratified random sampling. These are distinct, non-overlapping subgroups within your population, created based on specific attributes or characteristics. Strata allow you to categorize the population into more homogeneous groups, which is essential when dealing with diversity or variations in the attributes of interest.

For example, if you're conducting a customer satisfaction survey for a fast-food chain, you might create strata based on age groups (e.g., teenagers, adults, seniors) to ensure you capture the opinions of each demographic separately.

Sampling Units

Sampling units are the individual elements or entities within each stratum that are eligible for inclusion in your sample. These could be people, households, products, or any other units relevant to your research.

In a study focused on product preferences among consumers, your sampling units might be individual consumers within each age group (stratum). Accurate identification and selection of appropriate sampling units are essential to maintaining the integrity of your sample.

Proportional vs. Disproportional Stratified Sampling

When determining how to allocate sample sizes to each stratum, you have two primary options: proportional stratified sampling and disproportional stratified sampling.

• In proportional stratified sampling, the sample size for each stratum is determined in proportion to its size in the overall population. This approach ensures that larger strata have a bigger representation in your final sample, reflecting their prevalence in the population.
• Conversely, disproportional stratified sampling allocates sample sizes unequally among strata. You might opt for this approach when certain strata are of particular interest or when you want to ensure sufficient representation of smaller but critical subgroups.

For instance, if you are studying voter preferences in a city with multiple neighborhoods, you might use disproportional stratified sampling to allocate more samples to neighborhoods with diverse political leanings. This approach helps you capture a nuanced understanding of voting patterns.

Understanding these key concepts is crucial as they form the foundation upon which you'll build your stratified random sampling methodology. Now, let's move on to the practical steps involved in conducting this sampling technique.

How to Conduct Stratified Random Sampling?

Now that we've established a solid understanding of the core concepts, let's walk through the practical steps of conducting stratified random sampling. These steps provide a roadmap to help you execute the technique effectively in your research endeavors.

1. Define the Population

The initial step in stratified random sampling involves defining the population you intend to study. This definition should be crystal clear and align with your research objectives.

Consider the following when defining your population:

• Boundaries: Clearly specify the boundaries of your population. Are you studying all residents of a city, only those within a specific age range, or perhaps a subset defined by other criteria?
• Characteristics: Identify the key characteristics or attributes that define your population. These attributes will often guide the creation of strata later in the process.

For example, if you're interested in understanding the job satisfaction of IT professionals in a particular region, your population would be IT professionals in that region.

2. Create the Sampling Frame

With your population defined, the next step is to create a comprehensive sampling frame. The sampling frame is essentially a list or source that includes all the individual elements or entities within your defined population.

Ensure that your sampling frame is:

• Complete: It should encompass all members of the population without omission.
• Up-to-Date: Keep your sampling frame current to reflect any changes or additions to the population.
• Error-Free: Minimize errors, duplications, or inaccuracies in your sampling frame to prevent biases in your sample selection.

For instance, if your population consists of registered voters in a district, your sampling frame would be the official voter registration list for that district.

3. Identify and Define Strata

Once you have your sampling frame in place, it's time to identify and define the strata within your population. Strata are created based on specific attributes or characteristics relevant to your research.

Consider the following when defining strata:

• Homogeneity: Each stratum should represent a relatively homogeneous subgroup with respect to the chosen characteristic.
• Exclusivity: Strata should be mutually exclusive, meaning that each element in your population falls into one and only one stratum.
• Exhaustiveness: The sum of all strata should encompass the entire population.

For example, if you're studying income levels in a city, your strata might be defined as low-income, middle-income, and high-income households. Each household in the city would belong to one of these strata based on its income.

4. Determine the Sample Size for Each Stratum

One of the critical decisions in stratified random sampling is determining the sample size for each stratum. The sample size allocation should be proportional to the size of each stratum in the population.

You can calculate the sample size (nh) for each stratum (h) using the following formula:

nh = (Nh / N) * n

Where:

• nh = Sample size for stratum h
• Nh = Population size of stratum h
• N = Total population size
• n = Total desired sample size

This formula ensures that larger strata are allocated a larger sample size, reflecting their weight in the overall population.

For example, if you're conducting a survey in a city with three income strata and a total desired sample size of 300 respondents, the formula will help you determine how many respondents to survey in each income group.

5. Randomly Select Samples from Each Stratum

With sample sizes determined, you can now randomly select samples from each stratum. The fundamental principle here is randomness, as it ensures that every element within a stratum has an equal chance of being included in the sample.

You can use randomization methods such as random number generators or statistical software to select your samples within each stratum. Be sure to maintain the integrity of the randomization process to avoid biases.

6. Combine Stratum Samples to Form the Final Sample

Once you've sampled from each stratum, it's time to combine the stratum samples to create your final representative sample of the entire population. This final sample will provide you with valuable data for analysis and inference.

Achieving accurate representation in your research hinges on effective data collection. Appinio streamlines the process, providing comprehensive insights while ensuring your sample reflects the diversity of your population. By telling you everything about significance and delivering representative samples, Appinio empowers you to make informed decisions based on reliable data.

Ready to elevate your research game? Book a demo today and discover how Appinio can revolutionize your approach to data collection!

Stratified Random Sampling Advantages and Disadvantages

Stratified random sampling is a powerful tool, but like any method, it comes with its own set of advantages and disadvantages. Understanding these can help you make informed decisions about when and how to use this technique in your research.

Stratified Random Sampling Advantages

Here are the key advantages of stratified random sampling:

• Increased Precision: By dividing the population into strata based on relevant characteristics, stratified sampling reduces sampling error. This results in more precise estimates and greater statistical power.
• Enhanced Representation: Stratification ensures that all subgroups of interest are adequately represented in your sample. This is particularly valuable when you want to draw conclusions about specific demographic groups or subsets of your population.
• Efficient Resource Allocation: When you have limited resources, such as time or budget, stratified sampling allows for more efficient resource allocation. You can allocate a more significant portion of your resources to strata that are more critical to your research objectives.
• Improved Comparisons: Stratified random sampling makes it easier to compare and analyze data across different strata. This can lead to more meaningful insights, especially in studies where strata represent distinct groups with unique characteristics.
• Better Insights into Variability: Stratified sampling can highlight variations and patterns within different strata, enabling you to identify trends or differences that might be masked in a simple random sample.

For example, in a nationwide survey on healthcare satisfaction, stratified sampling would ensure that each age group, income level, and region is adequately represented in the sample. This enables you to make precise conclusions about the satisfaction of specific demographics.

Stratified Random Sampling Disadvantages

Despite its advantages, stratified random sampling has its share of disadvantages:

• Complexity: Stratified sampling requires careful planning, accurate stratification, and precise allocation of sample sizes. This complexity can be time-consuming and may necessitate specialized statistical software or expertise.
• Assumption of Homogeneity: The method assumes that each stratum is internally homogeneous, meaning that all members within a stratum share similar characteristics. In reality, there may be variations within strata that the method cannot capture.
• Difficulty in Identifying Strata: Identifying meaningful and relevant stratification variables can be challenging. Selecting the wrong variables or failing to capture the true diversity in the population can lead to biased results.
• Resource Intensive: While it can be efficient in terms of resource allocation, stratified random sampling may still require a larger sample size than simple random sampling to achieve the same level of precision. This can be resource-intensive, particularly in studies with many strata.
• Nonresponse Challenges: Managing nonresponse and ensuring that all selected individuals within a stratum participate can be more challenging in stratified sampling, as it involves multiple sampling stages.

To mitigate these disadvantages, careful planning, meticulous execution, and a clear understanding of your research objectives are essential. Stratified random sampling is a valuable tool when used appropriately, but it may not always be the best fit for every research scenario. It's necessary to weigh these advantages and disadvantages when deciding on your sampling strategy.

Practical Considerations in Stratified Random Sampling

Now that you understand the fundamentals and the pros and cons of stratified random sampling, let's explore practical considerations that will help you implement this technique effectively in your research.

Stratification Variables

Stratification variables are the characteristics or attributes you choose to create strata within your population. Selecting the correct stratification variables is crucial to the success of your sampling process. Here are some important considerations:

• Relevance: Stratification variables should be relevant to your research question and objectives. They should directly relate to the phenomenon you are studying. For example, if you're researching consumer preferences for smartphones, relevant stratification variables could include age, income, or brand loyalty.
• Mutually Exclusive Categories: Ensure that the categories within each stratification variable are mutually exclusive. Each element in your population should belong to one and only one stratum. For instance, if you're stratifying by age groups, avoid overlapping categories like "18-25" and "20-30."
• Diversity Representation: Strive to capture the diversity within your population. If a single stratification variable doesn't fully represent the complexity of your population, consider using multiple stratification variables to create a more nuanced picture.
• Practicality: While creating meaningful strata is important, be mindful of the practicality of collecting data within each stratum. Ensure you can effectively access and survey individuals or entities within each stratum.

Sampling Methods within Strata

Once you've established your strata, you'll need to consider the sampling methods within each stratum. Here are some factors to take into account:

• Randomness: Maintain the principle of randomness within each stratum. Whether you're using simple random sampling, systematic sampling, or another method, ensure that every element within the stratum has an equal chance of being selected.
• Sampling with or without Replacement: Decide whether your sampling within strata will be done with or without replacement. Sampling without replacement means that once an element is selected, it is not put back into the stratum. Sampling with replacement allows the same element to be selected more than once.
• Method of Randomization: Choose a reliable method of randomization. This could involve using random number generators, statistical software, or physical methods like drawing lots or using a random number table.
• Sample Size Determination: Remember that the sample size within each stratum should be determined based on the formula mentioned earlier to maintain the proportionality of your sample.

For example, suppose you're conducting a customer satisfaction survey within different age groups. In that case, you might use systematic sampling within each stratum to ensure a random yet evenly-spaced selection of respondents.

Nonresponse and Handling Missing Data

Addressing nonresponse and handling missing data is a critical aspect of stratified random sampling. Nonresponse occurs when selected individuals or entities within a stratum decline to participate in your survey or study. Here's how to handle it:

• Preventive Measures: Implement strategies to minimize nonresponse, such as clear and concise survey invitations, follow-up reminders, and incentives for participation.
• Imputation: When you encounter missing data, consider using imputation techniques to estimate the missing values. Imputation methods include mean imputation, regression imputation, and multiple imputation.
• Weighting: Apply weights to the data to account for nonresponse. This helps adjust the sample to better represent the population despite missing data.

Handling nonresponse effectively is crucial for maintaining the validity and representativeness of your sample.

Cost and Resource Constraints

Consider your budget and resource constraints when implementing stratified random sampling. While this method can be efficient in resource allocation, you must balance your research objectives with available resources. Here are some tips:

• Optimize Sample Size: Make strategic decisions about the total sample size and sample size allocation to ensure you obtain meaningful results without exceeding your budget or time constraints.
• Prioritize Strata: Allocate resources to strata that are most crucial to your research objectives. If certain strata are of greater interest, consider increasing the sample size for those strata while reducing it for less critical ones.
• Evaluate Costs: Conduct a cost-benefit analysis to assess the trade-offs between the precision of your results and the resources required. This analysis can help you make informed decisions.

Sample Size Allocation Strategies

When allocating sample sizes to each stratum, you have options beyond proportional allocation. Consider the following sample size allocation strategies:

• Proportional Allocation: Allocate sample sizes in proportion to the size of each stratum in the population, as discussed earlier.
• Equal Allocation: Allocate the same sample size to each stratum, regardless of their size. This approach ensures equal representation but may result in less precise estimates for smaller strata.
• Disproportional Allocation: Allocate sample sizes unequally among strata, prioritizing larger sample sizes for strata of greater research interest. This strategy can provide more precise estimates for critical subgroups.
• Optimal Allocation: Use mathematical optimization techniques to determine the sample sizes that minimize the overall variance of your estimates, given resource constraints.

Choosing the right sample size allocation strategy depends on your research objectives, budget, and the importance of various strata in your study.

By carefully considering these practical considerations, you can navigate the complexities of stratified random sampling and design a sampling strategy that aligns with your research goals while efficiently utilizing your available resources.

Stratified Random Sampling Examples and Applications

To gain a deeper appreciation for the versatility and real-world applicability of stratified random sampling, let's explore several examples and domains where this sampling method plays a crucial role.

Healthcare Surveys

Healthcare surveys frequently rely on stratified random sampling to ensure that data collection accurately represents diverse patient populations. Here are some ways stratified sampling is applied in healthcare:

• Patient Satisfaction Surveys: Hospitals and healthcare providers often use stratified sampling to collect feedback from patients. Strata may be defined by factors like age, medical condition, or length of hospital stay. This allows providers to address the unique needs of different patient groups.
• Clinical Trials: In clinical research, stratified random sampling helps ensure that participants from various demographics are included in clinical trials. This approach enables researchers to assess treatment efficacy and safety across different patient profiles.
• Epidemiological Studies: When studying disease prevalence or health behaviors in a population, stratification by age, gender, ethnicity, or geographic region ensures that the sample accurately represents the diversity of the population. This enhances the generalizability of findings.

Market Research

Stratified random sampling is a cornerstone of market research, helping companies gather valuable insights into consumer behavior and preferences. Here's how it's used in this field:

• Product Surveys: Companies often use stratified random sampling to survey customers about their preferences for products or services. Strata may be defined by factors such as age, income, or geographic location, allowing businesses to tailor their marketing strategies.
• Brand Loyalty Studies: When studying brand loyalty or customer satisfaction, stratified sampling ensures that customers from various demographic backgrounds are included. This approach provides a comprehensive view of customer sentiment.
• Market Segmentation: Market researchers use stratified random sampling to segment their target market into groups with similar characteristics. This helps businesses identify niche markets and develop tailored marketing campaigns.

Environmental Studies

Environmental scientists and researchers employ stratified random sampling to study diverse ecosystems and natural environments. Here's how it's used in environmental studies:

• Biodiversity Surveys: In studies of biodiversity, researchers stratify sampling sites based on factors like habitat type, elevation, or proximity to human activity. This ensures that the diversity of species is adequately represented in the sample.
• Water Quality Assessment: When assessing water quality in a river, lake, or ocean, stratified random sampling may be used to collect samples from different depths, locations, and seasons. This approach provides a more comprehensive understanding of water conditions.
• Wildlife Population Studies: Researchers studying wildlife populations often stratify by species, habitat, or geographical region. Stratified random sampling helps estimate the size and health of animal populations and assess threats to their survival.

Educational Research

Educational researchers use stratified random sampling to study student performance, educational interventions, and various aspects of the educational system. Here are examples of its application in this field:

• Student Achievement Studies: In educational research, stratified sampling allows researchers to select a representative sample of students from different grade levels, schools, or socioeconomic backgrounds. This helps evaluate factors influencing student achievement.
• Impact Assessment of Interventions: When assessing the effectiveness of educational interventions, researchers may stratify by intervention type, school size, or student demographics. This enables a more nuanced analysis of intervention outcomes.
• Teacher Surveys: Surveys of teachers and educators often use stratified random sampling to ensure that the views and experiences of teachers from various grade levels and subject areas are included, enhancing the reliability of the results.

These examples illustrate the versatility of stratified random sampling in various domains, highlighting its effectiveness in ensuring that research findings are both accurate and representative of the populations or phenomena under investigation.

Stratified Random Sampling Challenges

While stratified random sampling is a powerful method for obtaining representative samples, it's not immune to common mistakes and pitfalls. Being aware of these potential issues can help you avoid them and ensure the success of your sampling strategy.

Here are some common mistakes and pitfalls to watch out for:

1. Inadequate Stratification: Failing to create meaningful and relevant strata can lead to biased results. Ensure that your stratification variables accurately capture the diversity within your population.
2. Incorrect Allocation of Sample Sizes: Incorrectly allocating sample sizes to strata can impact the precision of your estimates. Be sure to follow the proportional allocation formula or your chosen allocation strategy meticulously.
3. Nonrandom Sampling within Strata: If randomization is not maintained within each stratum, the results may not accurately represent the stratum's characteristics. Ensure that the sampling method used within each stratum adheres to randomness principles.
4. Ignoring Nonresponse: Nonresponse can skew your results. Implement strategies to minimize nonresponse and consider the use of imputation techniques to handle missing data.
5. Overstratification: Creating too many strata can be counterproductive, as it may lead to small sample sizes within strata, reducing the precision of your estimates. Balance stratification with practical considerations.
6. Underestimating Resource Constraints: Be realistic about your budget and resource constraints. Stratified sampling, while efficient, can still require a larger overall sample size, which may exceed your available resources.
7. Ignoring Homogeneity Assumptions: While stratification assumes homogeneity within strata, some variability may exist. Be cautious when interpreting results, especially in strata with small sample sizes.
8. Failure to Update Sampling Frames: Using outdated or inaccurate sampling frames can introduce bias. Regularly update your frames to reflect changes in the population.
9. Overcomplicating the Sampling Process: While stratified sampling offers precision, overly complex designs can lead to operational challenges. Keep your sampling process manageable and straightforward.
10. Lack of Clear Research Objectives: Before implementing stratified sampling, define clear research objectives and questions. Without a solid foundation, you may struggle to create meaningful strata and allocate sample sizes effectively.
11. Inadequate Randomization Methods: Use reliable randomization methods within each stratum to ensure that every element has an equal chance of being selected. Avoid nonrandom or biased selection methods.

By being mindful of these common mistakes and pitfalls, you can navigate the complexities of stratified random sampling more effectively and increase the likelihood of obtaining accurate and representative results in your research.

Conclusion for Stratified Random Sampling

Stratified random sampling is a valuable method that allows researchers to obtain precise and representative data from diverse populations. By dividing the population into meaningful subgroups and selecting samples from each, you can ensure that your research findings are both accurate and applicable to specific demographics or characteristics of interest.

Remember, whether you're conducting healthcare surveys, market research, environmental studies, or educational research, the principles of stratified random sampling can help you make informed decisions and draw meaningful insights. By mastering this technique, you'll be better equipped to tackle research challenges and contribute valuable knowledge to your field.

How to Conduct Stratified Random Sampling in Minutes?

Appinio, the real-time market research platform, offers an exhilarating approach to conducting stratified random sampling for your market research needs. Imagine gaining crucial insights to drive your data-driven decisions within minutes without the need for a research PhD.

With Appinio, you'll experience:

• Speed and Precision: From questions to insights in a matter of minutes, Appinio ensures you don't miss a beat in your decision-making process.
• Accessible to All: Our platform's intuitive design makes it accessible to everyone, breaking down the barriers that traditional market research methods often present.
• Global Reach: Survey your target audience from over 90 countries, choosing from 1200+ characteristics to define the perfect group. Appinio takes the complexity out of reaching your global audience.

Register for free

Get free access to the platform!